Notas Técnicas

Sistemas Instrumentados de Seguridad – Parte 2

Hemos vista en el artículo anterior, algunos detalles del Ciclo de Vida de Seguridad y Análisis de Riesgo. Veremos ahora, algunos detalles sobre Ingeniería de Confiabilidad.

Confiabilidad de Sistemas de Mediciones

La confiabilidad en los sistemas de mediciones puede cuantificarse como el tiempo medio entre fallos ocurridos en el sistema. En este contexto, fallo significa la ocurrencia de una condición inesperada que causa un valor incorrecto en la salida.

Principios de Confiabilidad

Se puede cuantificar la confiabilidad de sistemas de mediciones como la habilidad del sistema para ejecutar su función dentro de límites y condiciones de funcionamiento dentro de un tiempo definido. Infelizmente, varios factores, tales como las tolerancias de los fabricantes según las condiciones de operación, dificultan a veces esta determinación, y en la práctica lo que se logra es expresar estadísticamente la confiabilidad a través de la probabilidad de fallos que ocurren en un cierto período.

Cuantificación de Confiabilidad

La confiabilidad es esencialmente de naturaleza probabilística y se puede cuantificar a través del tiempo medio entre fallos (MTBF – Mean Time Between Failures) y el tiempo medio hasta falla (MTTF – Mean Time To Failure). Hay que subrayar que estos dos indicadores son valores medios calculados a través de diferentes dispositivos, idénticos entre sí. Por lo tanto, para cualquier instrumento en particular los valores pueden ser distintos de la media.

El MTBF es un parámetro que expresa el tiempo medio entre fallos ocurridos en un instrumento, calculado en un determinado período. En casos en los cuales los equipos poseen alta confiabilidad, será difícil contarse el número de ocurrencias y podrán generar números imprecisos al MTBF. En dichos casos se recomienda usar el valor del fabricante.

El MTTF es una manera alternativa de cuantificarse la confiabilidad. Es normalmente utilizado en termopares, pues son descartados al fallar. El MTTF expresa el tiempo medio antes que ocurra el fallo, calculado en número idéntico de dispositivos.

La confiabilidad final asociada según la importancia al sistema de medición se expresa por el tiempo medio hasta reparación (MTTR – Mean Time To Repair), o sea, el tiempo medio para reparar un instrumento o aún el tiempo medio de sustitución de un equipo.

La combinación del MTBF y el MTTR muestra la disponibilidad:

Disponibilidad  = MTBF/ (MTBF+MTTR)

La disponibilidad mide la proporción de tiempo en el cual el dispositivo trabaja sin fallos.

El objetivo en sistema de mediciones es maximizar el MTBF y minimizar el MTTR y, consecuentemente, maximizar la disponibilidad.

Modelos de Fallos

El modelo de fallo de un dispositivo puede cambiar durante su ciclo de vida, permaneciendo inalterado, disminuyendo o aumentando.

En componentes electrónicos, es común ver el comportamiento visto en la figura 1, también conocido como “bathtub curve” (curva de la bañera)

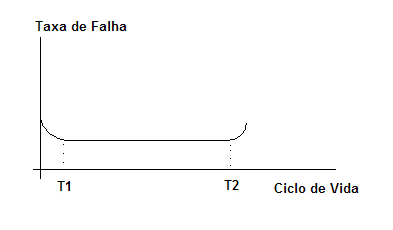Figura 1 – Curva típica de la variación de confiabilidad de un componente electrónico

Los fabricantes generalmente aplican pruebas de burn-in de manera de eliminarse la etapa T1 hasta que los productos sean distribuidos en el mercado.

Por otro lado, los componentes mecánicos presentarán una tasa de fallo más grande en el final de su ciclo de vida, de acuerdo con la figura 2.

Figura 2 – Curva típica de la variación de confiabilidad de un componente mecánico

En la práctica, los sistemas son composiciones electrónicas-mecánicas, y los modelos de fallos son complejos. Cuanto más componentes, mayor la incidencia y probabilidad de fallos.

Leyes de la confiabilidad

Existen diversos componentes en la confiabilidad, y el sistema para cuantificarla es complejo. Podemos tener componentes en serie y en paralelo.

La confiabilidad de componentes en serie debe tener en cuente la probabilidad de fallos individuales en determinado período. Para un sistema de medición con n componentes en serie, la confiabilidad Rs es el producto de las confiabilidades individuales: Rs = R1xR2...Rn.

Suponga que haya un sistema de medición formado por un sensor, un elemento de conversión y un circuito de procesamiento de señal, cuyas confiabilidades sean 0.9, 0.95 e 0.99. En este caso la confiabilidad del sistema será 0.9x0.95x0.99 = 0.85.

La confiabilidad puede ser aumentada a través de componentes paralelos, lo que significa que el sistema fallará solo si todos los componentes fallan. En este caso la confiabilidad RS es dada por:

Rs = 1 – Fs, donde Fs es la no-confiabilidad del sistema.

La no-confiabilidad es Fs = F1xF2...F3.

Por ejemplo, en un sistema de medición segura existen tres instrumentos idénticos paralelos. La confiabilidad de cada uno es 0.95, y la del sistema es dada por:

Rs = 1 –[ (1-0.95)x(1-0.95)x(1-0.95)] = 0.999875

Cómo mejorar la confiabilidad de un sistema de medición

El intento práctico es minimizar el nivel de los fallos. Un requisito importante es garantizar que se conozca y actúe antes del tiempo T2 (figuras 1 y 2) cuando la frecuencia estadística de los fallos aumenta. Lo ideal es hacer que T (período o ciclo de vida) sea igual a T2 y los tiempos sin fallos aumenten.

Existen varias maneras de aumentar la confiabilidad de un sistema de medición:

• Elección de los instrumentos: se debe siempre estar atento a los instrumentos especificados, sus influencias relativas al proceso, los materiales, el ambiente, etc.
• Protección de los instrumentos: protegiendo los instrumentos adecuadamente se puede ayudar a garantizar nivel mayor de seguridad. Por ejemplo, los termopares deberían estar protegidos en condiciones adversas de funcionamiento.
• Calibración regular: la mayoría de los fallos pueden ser causados por derivas que alteran y generan salidas incorrectas. Entonces, según la buena práctica de la instrumentación se recomienda que periódicamente los instrumentos sean inspeccionados y calibrados.
• Redundancia: en este caso se tiene más de un equipo trabajando en paralelo y accionado, a veces, automáticamente. La confiabilidad mejora significativamente.

Sistemas de Seguridad y Confiabilidad

Los Sistemas de Seguridad monitorean la condición de valores y parámetros de una planta dentro de los límites operacionales, y bajo condiciones de riesgo deben generar alarmas y poner las instalaciones en condición segura o mismo de shutdown.

Observe que las condiciones de seguridad se deben seguir y adoptar en fábricas en que las mejores prácticas de funcionamiento e instalación son una obligación tanto de empleados como de directores. Vale recordar que el primer concepto referente a la legislación de seguridad es asegurar que todos los sistemas sean instalados y operados de manera segura, y el segundo es que instrumentos y alarmas relativos a la seguridad sean manejados con confiabilidad y eficiencia.

Los Sistemas Instrumentados de Seguridad (SIS) son responsables por la seguridad operacional, y garantizan las paradas de emergencia dentro de los límites considerados seguros, siempre que la operación sobrepase estos límites. El objetivo principal es evitar accidentes dentro y fuera de las fábricas, tales como incendios, explosiones, daños a los equipos, protección de la producción y la propiedad y, más aún, evitar riesgos de vidas o daños a la salud de la personas e impactos catastróficos a la comunidad. Se debe tener en mente que ningún sistema es totalmente inmune a fallos y siempre deben proporcionar una condición segura, mismo en caso de fallo.

Métricas utilizadas en el campo de Ingeniería de la Confiabilidad relativa al SIS

1. Confiabilidad R(t)

La confiabilidad es una métrica desarrollada para determinar la probabilidad de éxito de una operación en determinado período de tiempo.

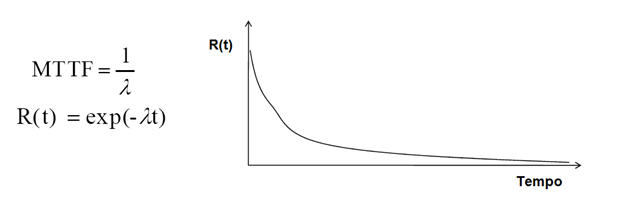Figura 3 – Confiabilidad R(t)

2. MTTR – Tiempo Medio de Reparo

La medición de confiabilidad exige que un sistema sea exitoso funcionando durante determinado tiempo. En este sentido, aparece la métrica del MTTR, que es el tiempo en lo cual se identifica un fallo y se lo repara (o restablece la normalidad operacional).

La tasa de restablecimiento del éxito operacional es dada por: µ = 1/MTTR.

En la práctica no es tan simple estimar esta tasa, principalmente cuando las actividades de inspección no son periódicas, pues el fallo puede ocurrir luego de una inspección.

3. MTBF – Tiempo Medio entre fallos

El MTBF es una medida básica de confiabilidad en artículos reparables de un equipo y se puede expresar en horas o años. Se usa normalmente en análisis de confiabilidad y sustentabilidad en sistemas y se puede calcular por la siguiente fórmula:

 MTBF = MTTR + MTTF

Donde:

• MTTR = Tiempo Medio de Reparo
• MTTF = Tiempo Medio para Fallar = el inverso de la suma de todas las tasas de fallos

Como el MTTR es muy pequeño en la práctica, es común asumir MTBF = MTTF

4. Disponibilidad A(t) e Indisponibilidad U(t)

Otra métrica muy útil es la disponibilidad. Se define como la probabilidad de que un dispositivo esté disponible (sin fallos) cuando, en un tiempo t, se exige que el mismo funcione dentro de las condiciones normales para las que fue proyectado.

Indisponibilidad es dada por: U(t) = - A(t)

La disponibilidad es función no solo de la confiabilidad, sino que también es función del mantenimiento. La Tabla 1 abajo muestra la relación entre confiabilidad, mantenimiento y disponibilidad. Observe en esta tabla que un aumento en la capacidad de mantenimiento implica una disminución del tiempo necesario para realizar acciones de mantenimiento.

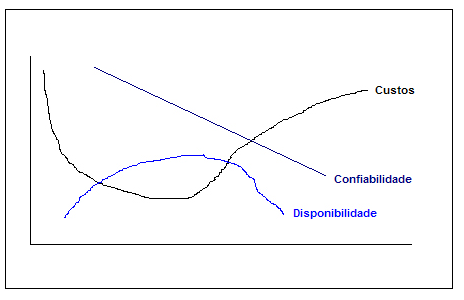Figura 4 – Confiabilidad, Disponibilidad y Costos

5. Probabilidad de Fallo en Demanda (PFDavg) y Prueba e Inspección Periódicos

PFDavg es la probabilidad de falla en un sistema de prevención de fallos. El nivel de SIL está relacionado con esta probabilidad y con el factor de reducción de riesgo (por cuanto es necesario proteger para garantizar un riesgo aceptable si ocurre un fallo).

PFD es el indicador de confiabilidad adecuado para sistemas de seguridad.

Sin ser sometido a prueba, la probabilidad de fallo tiende a ser 1.0 con el tiempo. Pruebas periódicas mantienen la probabilidad de fallo bajo límites deseables.

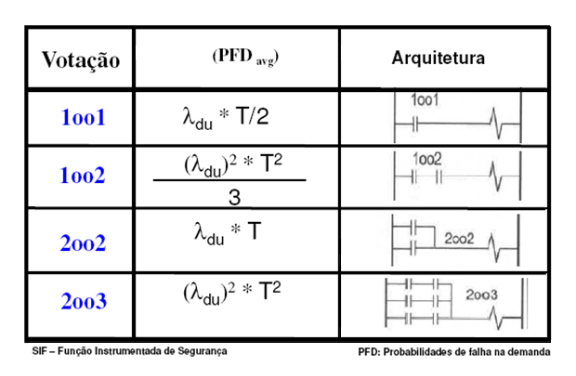Figura 5 – Votación, PFD y Arquitectura

La figura 5 muestra detalles de arquitectura versus votación y PFD, y la figura 6 muestra la relación entre el PFD y el Factor de Reducción de Riesgo.

Figura 6 – Relación entre el PFDavg y el Factor de Reducción de Riesgo

La Probabilidad de Fallo puede calcularse a través de la siguiente ecuación:

PFAvg = (Cpt x l x TI/2) + ((1-Cpt) x l x L xT/2), donde:

• l: tasa de fallo
• Cpt: porcentaje de fallos detectado por una prueba (proof test)
• TI: período de prueba
• LT: tiempo de vida de una unidad de proceso

Veamos un ejemplo: supongamos que una válvula es usada en un sistema instrumentado de seguridad y tiene una tasa de fallo anual de 0.002. A cada año se hace una prueba de verificación e inspección. Se estima que 70% de los fallos se detectan en estas pruebas. Esta válvula será utilizada durante 25 años y su demanda de uso es estimada a cada 100 años. ¿Cual la probabilidad media de fallo?

Usando la ecuación anterior tenemos:

 l: 0.002

Cpt: 0.7

TI: 1 año

LT: 25 años

PFDavg = (0.7) x 0.002 x ½ + (1-0.7) x 0.002 x 25/2 = 0.0082

Conclusión

En términos prácticos lo que se busca es la reducción de fallos y consecuentemente de paradas y riesgos operacionales. Se busca el aumento de disponibilidad y también, en términos de procesos, la minimización de variabilidad con consecuencia directa en el aumento de rentabilidad.

>> Si requiere más información, contáctenos vía mail a: info@escoarg.com.ar, o telefonicamente: (11) 2120-4500.